すでに何度か述べた用語で「関数」がありました。実は、この関数はプログラミング言語を学習する上で非常に重要なものです。
それでは、ここでは関数によるモジュール（部品）化を学習しましょう。

3.5.1　モジュール化

まずはモジュールとは、「電子機器などを構成する１つの単位で、機能が独立しており交換が可能なもの。車だったらタイヤ、エンジンなどの部品。」と定義できます。
つまり、大きなシステムの中の「部品」です。部品は多くの場合交換可能で、例えば自動車のタイヤは別の車種でも使えますよね（エンジンは無理かもしれませんが）。

プログラミングにおけるモジュール化の利点は次の2点です。

1. 他のプログラムに再利用できる
2. プログラムが見やすくなる

この、モジュール化された部品をプログラミングの世界では関数（function）と呼びます。一見、関数という言葉からはその性質をイメージしづらいですが、英語名のfunction（機能）からはその性質が想像しやすいですよね。
プログラム中の関数のイメージは【図3.5-b】になります。メインのプログラム内で関数がそのつど実行されます。

関数の構文です。

型　関数名( 型　引数, 　型　引数,　型　引数 ・・・)

引数という、関数に値を渡すための変数がありますが、この引数はいくつでも設定できます。
実は、あなたはすでに関数を使っています。例えばellipse()がそうです。
この構文はellipse(x, y, width, height)となっていて、座標と幅、高さを入力すると円を描いてくれる関数なのです。
Processingを含めたプログラミング言語は、膨大な関数群によって動いているのです。

3.5.2　関数の自作

さて、ellipse()などは、Processingの開発者側が用意した関数ですが、これらは自作することもできます。
それではまず簡単な関数を自作してみましょう。次は、円を描くサンプルです。

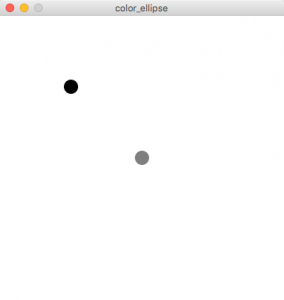
void setup() {
  size(400, 400);  //画面サイズ
  background(255);  //画面の色を更新
  noStroke();  //縁は描かない

  fill(0);  //黒の
  ellipse(100, 100, 20, 20);  //円を描く
  fill(127);  //グレーの 
  ellipse(200, 200, 20, 20);  //円を描く
}

fill()とellipse()が2回実行されています。よく見ると、色と座標が違うだけで大きさが一緒です。ここで、色のついた円を描く関数を作ってみましょう。

void colorEllipse(int _c, int _x, int _y){
 fill(_c);  //変数cに割り当てられた色の
 ellipse(_x, _y, 20, 20);  //円を描く  
 }

この( )の中のint _c, int _x, int _yは引数と呼ばれます。ここに色々な値を入れていくのです。
関数を作ったら、これを実際に使ってみます。すると、次のような形になります。

void setup() {
  size(400, 400);  //画面サイズ
  background(255);  //画面の色を更新
  noStroke();  //縁は描かない

  //黒の円を描く関数を実行
  colorEllipse(0, 100, 100);  
  
  //グレーの円を描く関数を実行
  colorEllipse(127, 200, 200);
}

void colorEllipse(int _c, int _x, int _y) {
  fill(_c);  //変数cに割り当てられた色の
  ellipse(_x, _y, 20, 20);  //円を描く
}

しかし、これだけではcolorEllipse関数を使わない状態との差があまりよく分かりません。もう少し拡張してみましょう。次は、大小2つの円が重なって描かれる関数を作って利用してみます。

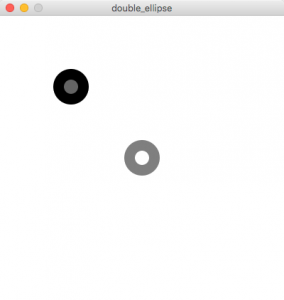
void setup() {
  size(400, 400);  //画面サイズ
  background(255);  //画面の色を更新
  noStroke();  //縁は描かない

  //黒の円を描く関数を実行
  doubleEllipse(0, 100, 100, 100);
  
  //グレーの円を描く関数を実行
  doubleEllipse(127, 255, 200, 200);
}

void doubleEllipse(int _c1, int _c2, int _x, int _y) {
  fill(_c1);  //変数c1に割り当てられた色の
  ellipse(_x, _y, 50, 50);  //外側の円を描く 

  fill(_c2);  //変数c2に割り当てられた色の
  ellipse(_x, _y, 20, 20);  //内側の円を描く
}

こうすると、円の数を増やしていくときも、doubleEllipse()の数を増やしていくだけになり、機能も分かりやすくコード自体も短くなります。

3.5.3　関数の型

さて、関数の宣言の前にvoidとありましたが、これは一体なんでしょう。よく考えてみると、setup関数やdraw関数の前にもvoidが書かれていました。
voidとは、「空（から）」という意味で、戻り値がないという意味なのです。
では、戻り値とは何でしょう。次のサンプルは、int型の戻り値をもつ関数の例です。

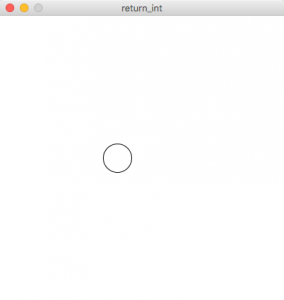
int x;  //x座標  
int velocity;  //円の移動スピード

void setup() {
  size(400, 400);  //画面サイズ
  velocity = 5;  //velocityの初期値を5に設定
  x = 0;
}

void draw() {
  background(255);

  //折り返しを判定する
  velocity = bounce(x, velocity);
  x += velocity;
  ellipse(x, height/2, 40, 40);
}

//折り返しを判定する関数
int bounce(int _x, int _velocity) {

  //x座標が画面幅を超えるか、0未満になったら
  if (_x > width || _x < 0) {
    _velocity = -_velocity;  //_velocityの値の正負を変更
  }
  return _velocity;  //int型の値を返す
}

上の例題では、x座標の折り返しの判定を行い、velocityの値をプラスにしたりマイナスにしたりする関数を作りました。計算結果はreturn _velocityで、int型の値を返します。これが戻り値なのです。

また、次はBoolean型の値を返す関数が使われているサンプルです。

int x, y;  // 円の位置
int eSize = 100;   // 円の直径

//マウスカーソルが円の中に入ったかを判定
boolean circleEnter = false;
int bgColor = 0;    //背景色の設定（初期値は黒）

void setup() {
  size(400, 400);
  background(0);
  noStroke();

  x = width/2;    //円は、画面の中央に表示
  y = height/2;
}

void draw() {
  background(bgColor);    //背景色を設定

  //もし、マウスカーソルが円の中に入ったら
  if (enterCircle(x, y, eSize)) {
    circleEnter = true;
    fill(200);    //円の色を200のグレーに変更
  } else {
    circleEnter = false;
    fill(100);    //そうでなかったら100のグレー
  }
  ellipse(x, y, eSize, eSize);    //円の描画
}

void mousePressed() {
  //もし、マウスカーソルが円の中に入ったら
  if (circleEnter) {

    //背景色が黒の場合は白、白の場合は黒に変更
    switch(bgColor) {
    case 0: 
      bgColor = 255; 
      break;
    case 255:  
      bgColor = 0; 
      break;
    }
  }
}

//マウスカーソルが円の中に入ったかどうかを判定する関数
boolean enterCircle(int _x, int _y, int _diameter) {
  //円の中心からの距離を算出
  if (dist(_x, _y, mouseX, mouseY) < _diameter/2) {
    return true;
  } else {
    return false;
  }
}

どうでしょうか？まずは概念だけでも理解しておきましょう。初めは自作することが難しくても、他人のコードが関数を使って書かれている場合に理解の助けになります。慣れてきたらどんどん関数を自作してみてください。