円グラフをプログラムで作ってみる

      円グラフをプログラムで作ってみる へのコメントはまだありません

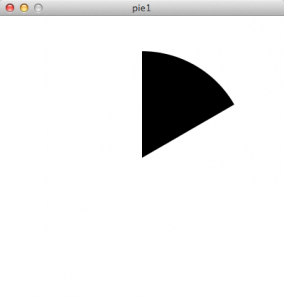
まずは、一つのパーツを描画してみます。円グラフの描画には、arc()関数を使います。

2013_07_04_20_52

1
2
3
4
5
6
7
8
9
10
11
12
13

float pie_w = 300;  //円グラフの幅
float pie_h = 300;  //円グラフの高さ
int lastAngle = -90;   //通常の円グラフの始点にするため、スタート地点を設定
int angle0 = 60;  //グラフの角度
 
size(400, 400);
background(255);
noStroke();
 
fill(0);
 
//中心点のx, 中心点のy, 幅, 高さ, 始点の角度, 終点の角度
arc(width/2, height/2, pie_w, pie_h, radians(lastAngle), radians(lastAngle + angle0));

 
 

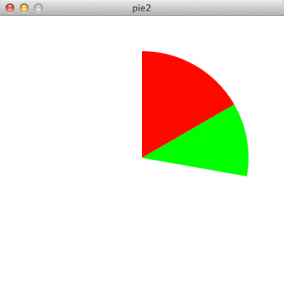
次に、もう一つ追加してみましょう。ポイントは、次のパーツを描画するときにはlastAngleに前のパーツのアングルを加算していく事です。

2013_07_04_20_57

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

float pie_w = 300;  //円グラフの幅
float pie_h = 300;  //円グラフの高さ
int lastAngle = -90;   //通常の円グラフの始点にするため、スタート地点を設定
int angle0 = 60;  //1つ目のグラフの角度
int angle1 = 40;  //2つ目のグラフの角度
 
size(400, 400);
background(255);
noStroke();
 
fill(255, 0, 0);  //赤
//中心点のx, 中心点のy, 幅, 高さ, 始点の角度, 終点の角度
arc(width/2, height/2, pie_w, pie_h, radians(lastAngle), radians(lastAngle + angle0));
 
lastAngle += angle0;  //lastAngleにangle0を足して、次のグラフの開始点にする
 
fill(0, 255, 0);  //緑
arc(width/2, height/2, pie_w, pie_h, radians(lastAngle), radians(lastAngle + angle1));

 
 

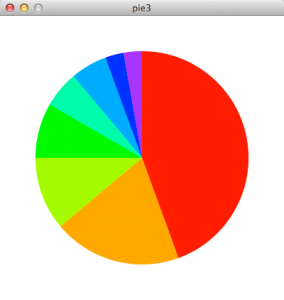
更に360°完全に埋めてみましょう。その場合には配列を使うと便利です。さらに、このサンプルでは、色も配列に入れてみています。

2013_07_04_23_57

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

float pie_w = 300;  //円グラフの幅
float pie_h = 300;  //円グラフの高さ
int lastAngle = -90;   //通常の円グラフの始点にするため、スタート地点を設定
int[] angle = { 160, 70, 40, 30, 20, 20, 10, 10 };  //グラフの角度
color[] pieColor = new color[angle.length];  //配列angleの項目数分のcolor配列を作成
 
size(400, 400);
background(255);
noStroke();
 
//colorModeをHSBに変更。色相=360°、彩度=100％、明度=100％
colorMode(HSB, 360, 100, 100);
 
for(int i = 0; i < angle.length; i ++){
  pieColor[i] =color(i*40, 100, 100);  //色相のみを40°変えてpiColorに格納
}
 
for (int i = 0; i < angle.length; i ++) {
  fill(pieColor[i]);  //赤
  //中心点のx, 中心点のy, 幅, 高さ, 始点の角度, 終点の角度
  arc(width/2, height/2, pie_w, pie_h, radians(lastAngle), radians(lastAngle + angle[i]));
 
  lastAngle += angle[i];  //lastAngleにangle[i]を足して、次のグラフの開始点にする
}

この円グラフのプログラムを応用して、ラベルを表示したりマウスオーバーで色が濃くなったりするインタラクションを追加してみます。

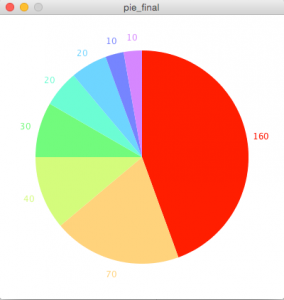
pie_final_and_円グラフをプログラムで作ってみる___Yasushi_Noguchi_Class

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

float pie_w = 300;  //円グラフの幅
float pie_h = 300;  //円グラフの高さ
int startAngle = -90;
int lastAngle = -90;   //通常の円グラフの始点にするため、スタート地点を設定
int[] angle = {160, 70, 40, 30, 20, 20, 10, 10};  //グラフの角度
color[] pieColor = new color[angle.length];  //配列angleの項目数分のcolor配列を作成
 
 
void setup() {
  size(400, 400);
  noStroke();
  textAlign(CENTER);
  smooth();
 
  //colorModeをHSBに変更。色相=360°、彩度=100％、明度=100％
  colorMode(HSB, 360, 100, 100);
 
  for (int i = 0; i < angle.length; i ++) {
    pieColor[i] =color(i*40, 50, 100);  //色相のみを40°変えてpiColorに格納
  }
}
 
void draw() {
  background(360, 0, 100);
 
  float mouseAngle = degrees(atan2(mouseY-height/2, mouseX-width/2));  //円の中心からのマウスの角度を計算
  float dist = dist(width/2, height/2, mouseX, mouseY);  //円の中心からのマウスの距離を計算
 
  //atan2()によって計算された角度が、-90度から270度になるように変更
  if (mouseAngle < startAngle) {
    mouseAngle += 360.0;
  }
 
  println("mouseAngle= " + mouseAngle);  //円の中心からのマウスの角度
  println("dist= " + dist);  //円の中心からのマウスの距離
 
  for (int i = 0; i < angle.length; i ++) {
 
 
    //距離が円の半径以内で、中心からのマウスの位置の角度がそれぞれの円弧の角度内かを調べる。
    if (dist < 150 && mouseAngle > lastAngle && mouseAngle < lastAngle + angle[i]) {
      fill(i*40, 100, 100);  //角度内だったら明度を100にする。
    }else {
      fill(i*40, 50, 100);  //外だったら明度を50にする。
    }
 
    //中心点のx, 中心点のy, 幅, 高さ, 始点の角度, 終点の角度
    arc(width/2, height/2, pie_w, pie_h, radians(lastAngle), radians(lastAngle + angle[i]));
    //fill(0, 0, 20);
    text(angle[i], width/2 + 170*cos(radians(lastAngle + angle[i]/2)), height/2 + 5 + 170*sin(radians(lastAngle + angle[i]/2)));
 
    lastAngle += angle[i];  //lastAngleにangle[i]を足して、次のグラフの開始点にする
    if (lastAngle >= startAngle + 360) lastAngle = startAngle;  //270度超えていたら-90度に戻す
  }
}