それでは、ここからは3Dプログラミングを体験してみます。Processingの場合、3Dの機能は基本的なものが実装されていますが、工夫次第では、2Dではできないような表現が可能になるでしょう。
5.1.1 まずは立体を描画してみる
まずは、基本的な3Dモデルである立方体(cube)を表示、コントロールするところから始めます。
ここでは、processing標準の3D描画機能であるP3Dを使います。
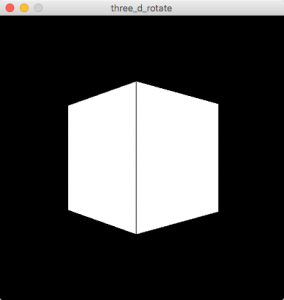
まず、立方体を表示します【図5.1-a】。
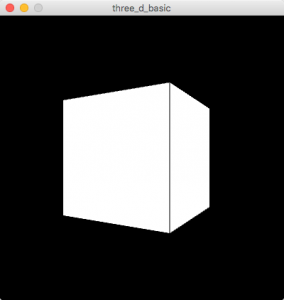
void setup() {
//P3Dと書くことによって、3Dを使うことを明示する
size(400, 400, P3D);
}
void draw() {
background(0);
translate(width/2, height/2); //立体の中心を画面中央に移動
//ラジアンで指定。Y軸に対して60度回転。2PI=360°なので、PI/3が60度
rotateY(PI/3);
box(150, 150, 150); //150 x 150 x 150pxの立方体を描画
}【リスト5.1-a】のコードを解説します。
サイズを宣言する際に、末尾に「P3D」を宣言します。
size(400, 400, P3D);次に、「translate」を使って、中心点を移動します。
translate(width/2, height/2);そして、Y軸を中心にして60度回転します。360°=2PIなので、60°=PI/3になります。
rotateY(PI/3);最後に、150 x 150 x 150pxの立方体を描画します。
box(150, 150, 150);5.1.2 x, y, z軸の理解
それでは、x, y, z軸の関係性を確認しましょう。3Dの場合はz軸が加わります。
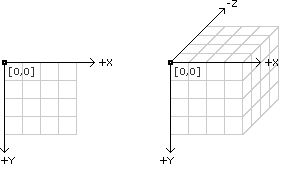
z軸の値を変えてみましょう。一見立方体が小さくなったかのようですが、これは視点から遠ざかっているのです。
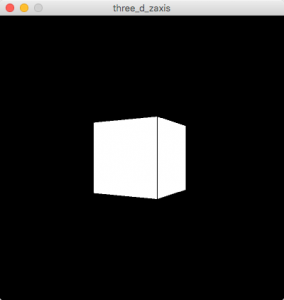
void setup() {
//P3Dと書くことによって、3Dを使うことを明示する
size(400, 400, P3D);
}
void draw() {
background(0);
//立体の中心を画面中央に移動し、奥行きを200pxを奥にする
translate(width/2, height/2, -200);
//ラジアンで指定。Y軸に対して60度回転。2PI=360°なので、PI/3が60度
rotateY(PI/3);
box(150, 150, 150); //150 x 150 x 150pxの立方体を描画
}5.1.3 座標系の移動(translate)
前述のサンプルでtranslate()を使いましたが、実は「4.1 座標変換」で2Dグラフィック作成の際にも使っています。3Dプログラミングでは、物体の移動は座標変換が基本になります。【図5.1-d】のグラフィックを描画してみましょう。このサンプルではfor文を使ってboxを複製しています。

translate()を使って移動させるのですが、これはオブジェクト単体を移動するのではなく、空間全体を移動するのでしたね。ですから、複数のオブジェクトが画面上にある場合はすべて移動します。
次のようにtranslate()を繰り返すと、その座標は加算されます。描画されるたびに基準点が変わります。
void setup() {
size(400, 400, P3D);
}
void draw() {
background(0);
//立体の中心を画面中央に移動
translate(width/2, height/2);
//立方体を、30ピクセルごとに5個生成
for (int i = 0; i < 5; i ++) {
translate(30, 0);
box(20, 20, 20); //20 x 20 x 20pxの立方体を描
}
}5.1.4 座標系の回転(rotate)
次は回転です。回転はrotate()を使います。
rotate()も、translate()と同じように空間全体を回転します。回転方向は【図5.1-e】のようになります。
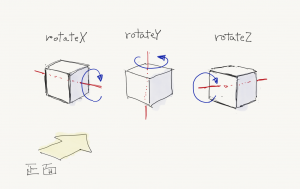
このサンプルはy軸を中心に回転しています【リスト5.1-d】。rotateX(), rotateZ()も使って、他の軸を基準にした回転も加えてみましょう。
float theta = 0.0; //角度
//2PIを360度で割っているのでradは度数法の1度。
float rad = TWO_PI/360.0;
void setup() {
size(400, 400, P3D);
}
void draw() {
background(0);
//立体の中心を画面中央に移動
translate(width/2, height/2);
rotateY(theta); //Y軸に対してangleの数値分だけ回転
box(150, 150, 150); //150x150x150pxの立方体を描
theta += rad; //時間を進める
//1周期分終わったら原点に戻る
if (theta > TWO_PI) theta = 0.0;
}5.1.5 座標系の拡大縮小(scale)
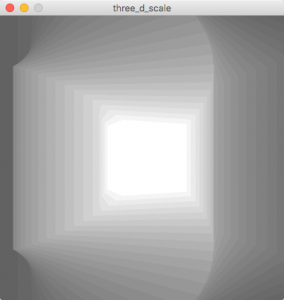
もちろん、scale()も使えます。引数は1.0が等倍なので、2倍の場合には2.0になります。3Dの場合でもフェード効果は適用できるので、フェードをかけてみました。見え方がかなり変わります。
float theta = 0.0; //角度
//2PIを360度で割っているのでradは度数法の1度。
float rad = TWO_PI/360.0;
void setup() {
size(400, 400, P3D);
background(0);
noStroke();
}
void draw() {
fade(true);
translate(width/2, height/2); //立体の中心を画面中央に移動
rotateY(theta); //Y軸に対してangleの数値分だけ回転
//sin(theta)の計算結果はは-1.0~1.0なので、+1,0で0.0~2.0になる
scale(sin(theta) + 1.0);
fill(255);
box(150, 150, 150); //150 x 150 x 150pxの立方体を描
theta += rad; //時間を進める
if (theta > TWO_PI) theta = 0.0; //1周期分終わったら原点に戻る
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(0, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
} else {
background(0);
}
}5.1.6 座標系の保存
次に、3Dグラフィックスにおける必須の概念である、座標系の保存(pushMatrix, popMatrix)です。実はこれも「4.1.5 pushMatrix, popMatrix(座標系の保存と呼び出し)」で体験しています。
・pushMatrix → 現在の座標系を保存する
・popMatrix → 保存した座標系を再展開する
でしたね。
それでは、このpushMatrix()とpopMatrix()を使って複製されたboxの座標を指定してみます。
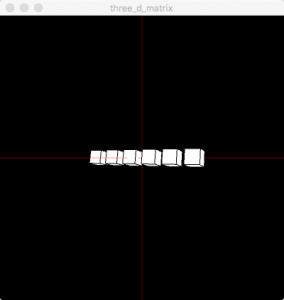
X軸方向に6個作成します。ポイントは、回転の中心軸を中央にすることです。
float boxSize = 20; //立方体のサイズ
float distance = 30; //立方体同士の距離
float halfDis; //立方体同士の一辺の全体の距離の半分
int boxNum = 6; //立方体の数
void setup() {
size(400, 400, P3D);
halfDis = distance*(boxNum - 1)/2; //6個並んだ際の距離の半分
}
void draw() {
background(0);
stroke(255, 0, 0, 100);
line(width/2, 0, width/2, height);
line(0, height/2, width, height/2);
translate(width/2, height/2); //立体の中心を画面中央に移動
rotateY(radians(mouseX));
rotateX(radians(mouseY));
stroke(0);
fill(255);
//立方体を、x軸方向に30ピクセルごとに並べて6個生成
for (int x = 0; x < boxNum; x ++) {
pushMatrix();
translate(x*distance - halfDis, 0, 0);
box(boxSize, boxSize, boxSize); //20x20x20pxの立方体を描く
popMatrix();
}
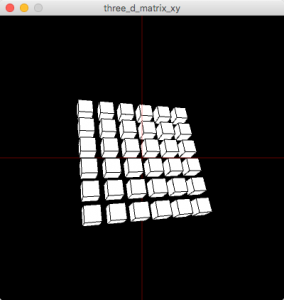
}次にy方向にも複製します。
float boxSize = 20; //立方体のサイズ
float distance = 30; //立方体同士の距離
float halfDis; //立方体同士の一辺の全体の距離の半分
int boxNum = 6; //立方体の数
void setup() {
size(400, 400, P3D);
halfDis = distance*(boxNum - 1)/2; //6個並んだ際の距離の半分
}
void draw() {
background(0);
stroke(255, 0, 0, 100);
line(width/2, 0, width/2, height);
line(0, height/2, width, height/2);
translate(width/2, height/2); //立体の中心を画面中央に移動
rotateY(radians(mouseX));
rotateX(radians(mouseY));
stroke(0);
fill(255);
//立方体を、x, y軸方向に30ピクセルごとに並べて6個生成
for (int y = 0; y < boxNum; y ++) {
for (int x = 0; x < boxNum; x ++) {
pushMatrix();
translate(x*distance - halfDis, y*distance - halfDis, 0);
box(boxSize, boxSize, boxSize); //20x20x20pxの立方体を描く
popMatrix();
}
}
}
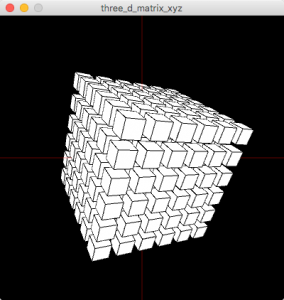
この要領でz方向にも複製します。
float boxSize = 20; //立方体のサイズ
float distance = 30; //立方体同士の距離
float halfDis; //立方体同士の一辺の全体の距離の半分
int boxNum = 6; //立方体の数
void setup() {
size(400, 400, P3D);
halfDis = distance*(boxNum - 1)/2; //6個並んだ際の距離の半分
}
void draw() {
background(0);
stroke(255, 0, 0, 100);
line(width/2, 0, width/2, height);
line(0, height/2, width, height/2);
translate(width/2, height/2); //立体の中心を画面中央に移動
rotateY(radians(mouseX));
rotateX(radians(mouseY));
stroke(0);
fill(255, 255, 255);
//立方体を、x, y, z軸方向に30ピクセルごとに並べて6個生成
for (int z = 0; z < boxNum; z ++) {
for (int y = 0; y < boxNum; y ++) {
for (int x = 0; x < boxNum; x ++) {
pushMatrix();
translate(x*distance - halfDis, y*distance - halfDis, z*distance - halfDis);
box(boxSize, boxSize, boxSize); //20x20x20pxの立方体を描く
popMatrix();
}
}
}
}5.1.7 回転した座標系の保存
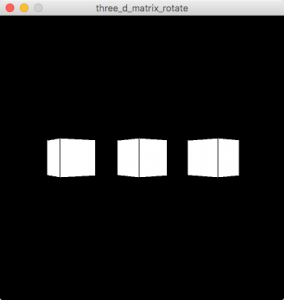
回転(rotate)の場合もtranslate()と考え方は一緒です。一つのオブジェクトを回転させるたびに、pushMatrix()とpopMatrix()を使うと、x, y, z座標はそのままでそれぞれのオブジェクトが回転します。
void setup() {
size(400, 400, P3D);
}
void draw() {
background(0);
for (int i = 0; i < 3; i++) {
pushMatrix();
translate((i + 1)*100, height/2); //立体の中心を移動
rotateY(radians(mouseX)); //y軸に対してangleの数値分だけ回転
box(50, 50, 50); //50x50x50pxの立方体を描
popMatrix();
}
}
5.1.8 vertex(頂点)を使用した図形の描画
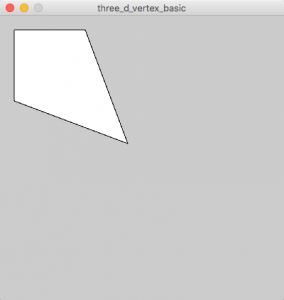
ここでは、vertex(頂点)を使用して図形を自作してみます。サンプルは分かりやすくするために基本図形を使っていますが、vertexを使うと様々な形の図形を描くことができます。まずは、beginShape()で形を描くことを宣言しvertex(x, y)で一つずつ頂点を指定します。
vertexの描画には次のルールがあります。
・vertexの頂点をつなぐ順番は時計回りでも反時計回りでもいい
・何点でも作ることができる
・endShape(CLOSE)で図形を閉じる
size(400, 400, P3D);
beginShape();
vertex(20, 20);
vertex(120, 20);
vertex(180, 180);
vertex(20, 120);
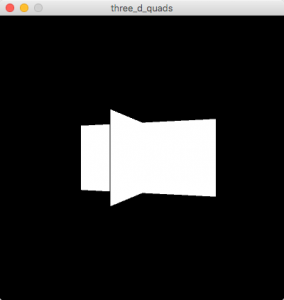
endShape(CLOSE);次に、vertexで四角形を描いてみます。QUADSを宣言する場合には、必ずvertexの数が4の倍数になるようにしましょう。
void setup() {
size(400, 400, P3D);
}
void draw() {
background(0);
translate(width/2, height/2); //立体の中心を画面中央に移動
//y軸に対してマウスのX軸の動きによって角度を変える
rotateY(radians(mouseX));
fill(255);
beginShape(QUADS); //四角形を描くことを宣言する
//正面
vertex(100, 50, 0); //一点ずつ順番に座標を指定する
vertex(100, -50, 0);
vertex(-100, -50, 0);
vertex(-100, 50, 0);
//縦
vertex(0, 50, 100); //一点ずつ順番に座標を指定する
vertex(0, -50, 100);
vertex(0, -50, -100);
vertex(0, 50, -100);
endShape(); //四角形を閉じる
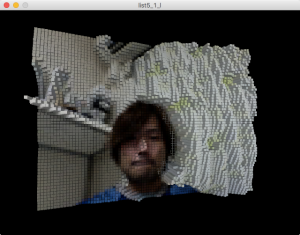
}5.1.9 リアルタイム映像と3D
3Dグラフィックスとビデオライブラリを組み合わせると、取り込んだ映像を立体的に表示できたりもします。興味がある人は自分で勉強してみましょう。
注意! 以下のサンプルは2020年6月現在、macOS Catalinaではエラーが出ます。Windowsでは動くと思います。
import processing.video.*; //ビデオのライブラリをインポート
Capture video;
void setup() {
size(640, 480, P3D);
video = new Capture(this, 80, 60, 60);
noStroke();
video.start();
}
void draw() {
lights();
background(0);
//画面中央にオブジェクトがくるように移動する
translate(width/2, height/2, -200.0);
//マウスの動きによって角度が変わる。
rotateX(radians(-mouseY));
rotateY(radians(mouseX));
if (video.available()) { //もしキャプチャができたら、
video.read(); //ビデオフレームの読み込み
video.loadPixels(); //ビデオのピクセルを操作できるようにする
//1ピクセルごとに色を調べる。
for (int y = 0; y < video.height; y ++) {
for (int x = 0; x < video.width; x ++) {
//ビデオのピクセルを抜き出す
int pixelColor = video.pixels[y*video.width + x];
//赤、緑、青をそれぞれ抽出する。以下の3行はビットシフトといって、
//理解するのが結構大変なので、ここでは詳細は説明しない。
int r = (pixelColor >> 16) & 0xff;
int g = (pixelColor >> 8) & 0xff;
int b = pixelColor & 0xff;
pushMatrix(); //座標を保存
translate(x*8 - width/2, y*8 - height/2, 0.0);
fill(r, g, b); //色を適応させる
//直方体を作成。手前から奥の長さは、色によって変化する。最大値は300。
//黒のときに300、白のときに0になる。
box(7, 7, float((255 - r)*(255 - g)*(255-b))/pow(255.0, 3)*300.0);
popMatrix(); //座標を復帰
}
}
}
}