1次元配列はどうでしたか?次は2次元配列です。構造は実はシンプルなのですが、やはり1次元配列よりは複雑になります。
式としては、[]がもう一つ増えて、例えば、
int[][] a = new int[3][5];となります。
配列を宣言する際に、値を入れることができます。
//初期化の際に直接値を入れる。
//int[][] a = new int[3][5];と構造的には同じ
int[][] a = {{0, 1, 2, 3, 4},
{5, 6, 7, 8, 9},
{10, 11, 12, 13, 14}};
//0~2の値を入れれば、それぞれの行の値が出る
println(a[0]);この場合、画像処理のコードとも関連するので、次のように行と列の関係を覚えるといいでしょう【図4.3-h】。

図4.3-h
この式の配列の概念図は【図4.3-i】になります。つまり、3行 x 5列 = 15個の箱が作られるということです。この図にそれぞれの箱のインデックス番号を記載しています。
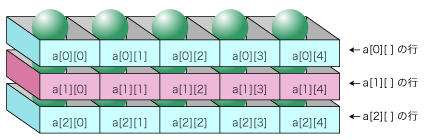
図4.3-i
それぞれの箱の値を変えたい時は、a[0][3] = 5 などのように値を代入してあげます。
4.3.6 2次元配列に円のサイズの値を格納する
では、実際にどの様に使うことできるのでしょうか。2次元配列は様々な用途に使えますが、ここでは簡単な参考例を示します。このサンプルは、3 x 5個の円の大きさの値を配列に格納しています。

図4.3-j
リスト4.3-f
float[][] eSize = new float[3][5]; //円のサイズ
size(400, 200);
background(255);
noStroke();
fill(0);
for (int y = 0; y < 3; y++) { //列方向
for (int x = 0; x < 5; x++) { //行方向
//円のサイズを10~100未満で決定
eSize[y][x] = random(10, 100);
ellipse(100 * x, 100 * y, eSize[y][x], eSize[y][x]); //円を描く
}
}次に、3 x 5個の円の拡大縮小のスピードが変わるアニメーションにしてみます。

図4.3-k
リスト4.3-g
float[][] eSize = new float[3][5]; //円のサイズ
//円の拡大縮小のスピード
float[][] speed = {{0.1, 0.5, 0.3, 0.2, 1.5},
{1.0, 2.0, 1.5, 2.0, 0.05},
{0.4, 0.8, 0.08, 1.1, 1.4}};
float minSize = 1.0; //円のサイズの最小値
float maxSize = 100.0; //円のサイズの最大値
void setup() {
size(400, 200);
background(255);
noStroke();
fill(0);
for (int y = 0; y < 3; y++) { //円のサイズを最小値に設定
for (int x = 0; x < 5; x++) {
eSize[y][x] = minSize;
}
}
}
void draw() {
background(255);
for (int y = 0; y < 3; y++) { //列方向
for (int x = 0; x < 5; x++) { //行方向
eSize[y][x] += speed[y][x]; //円のサイズを変化させる
//もし円のサイズが最大値を超えたか最小値未満になったら
//speedの増減を反転させる
if (eSize[y][x] > maxSize || eSize[y][x] < minSize)
speed[y][x] = -speed[y][x];
//円を描く
ellipse(100*x, 100*y, eSize[y][x], eSize[y][x]);
}
}
}このサンプルの特徴は、前述の15個の箱にそれぞれ独自の変数が設定されている点です。サンプルを実行してみると、それぞれの円の拡大縮小のスピードが全て違うことが分かるでしょう。この配列は、特に何次元までという制限はないので3次元でも4次元でも作ることができるのですが、実際に使うのは2次元配列までであることが多いので、ここでは2次元配列までしか説明しません。
この2次元配列は後述の「4.4 画像処理」の節でも使われます。
4.3.7 グラフィックへの応用
【リスト4.3-f】のサンプルは比較的シンプルなグラフィックですが、このアルゴリズムを応用して展開する事によって、様々なパターンを作ることができます。
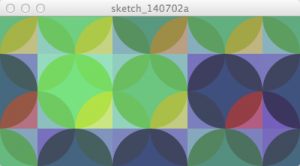
図4.3-l
リスト4.3-h
float[][] eColor = new float[3][5]; //円の色
//円の色の変化のスピード
float[][] speed = {{1.5, 2.5, 9.0, 7.2, 10.9},
{0.5, 2.0, 5.0, 4.0, 10.0},
{1.5, 12.0, 7.0, 1.0, 0.5}};
void setup() {
size(400, 200);
background(255);
noStroke();
fill(0);
rectMode(CENTER);
for (int y = 0; y < 3; y ++) {
for (int x = 0; x < 5; x ++) {
eColor[y][x] = 0; //円の色を黒に設定
}
}
}
void draw() {
background(255);
for (int y = 0; y < 3; y ++) {
for (int x = 0; x < 5; x ++) {
eColor[y][x] += speed[y][x]; //円の色を変化させる
//もし円の色が255を超えたか0未満になったら
//speedの増減を反転させる
if (eColor[y][x] > 255 || eColor[y][x] < 0)
speed[y][x] = -speed[y][x];
fill(0, eColor[y][x], 255, 127);
rect(x*100, y*100, 100, 100); //四角形を描く
fill(0, eColor[y][x], 0, 127);
ellipse(x*100, y*100, 100, 100); //円を描く
fill(255, eColor[y][x], 0, 127);
ellipse(x*100+50, y*100+50, 100, 100); //円を描く
}
}
}