すでに「3.4 インタラクション1」では、簡単なマウスイベントを学習しました。基本のインタラクションは次のコードになりますね。
図4.7-a
リスト4.7-a
void setup() {
size(400, 400);
noStroke();
fill(0);
}
void draw() {
background(255);
ellipse(mouseX, mouseY, 20, 20);
}また、マウスクリックによって円のx, y座標が更新されるサンプルです。
リスト4.7-b
int x, y; //x,y座標
void setup() {
size(400, 400);
noStroke();
fill(0);
x = 0; //x,yを0で初期化
y = 0;
}
void draw() {
background(255);
ellipse(x, y, 20, 20);
}
void mousePressed(){
x = mouseX; //x,yはマウスのx,y座標
y = mouseY;
}4.7.1 イージング
では、次に少し複雑なマウスイベントを見てみましょう。インタラクションとしては一般的なのですが、オブジェクトがマウスの位置に少し遅れてついてくるプログラムです。こういった動きのように、A点からB点へオブジェクト移動する時に動きに緩急をつけることをイージングと言います。イージングには様々な種類がありますが、ここでは基本的な動きのアルゴリズムを理解しておきましょう。
ここでは、その追跡のアルゴリズムを【図4.7-b】のように考えます。分かりやすくするため、x座標だけを扱います。
図4.7-b
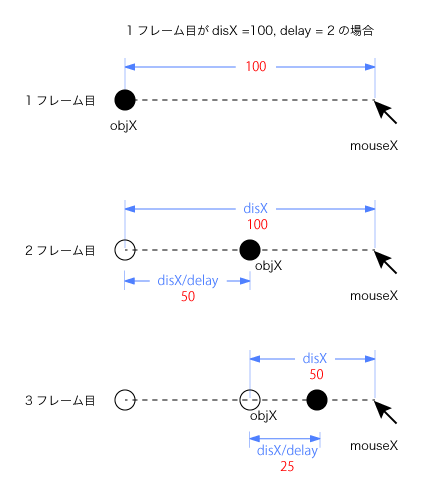
1フレーム目のdisX = 100、delay = 2.0だとするとdisX/delayは50になり、その値がobjXに加算されることによって2フレーム目にはオブジェクトが50ピクセル動きます。さらに、3フレーム目は、disXが50でdisX/delayは25になります。つまり、だんだん移動距離が少なくなっていくわけです。
よって、delayの値を大きくすればするほど、マウスに追随するスピードが遅くなります。
図4.7-c
リスト4.7-c
float objX, objY; //オブジェクトのx, y座標
float disX, disY; //mouse座標とオブジェクトの距離
//マウスに遅れる度合い（2.0だと速すぎて分かりにくいので20.0にしておく）
float delay = 20.0;
void setup() {
size(400, 400);
background(255); //背景は白
noStroke();
fill(0);
objX = mouseX; //objX, disXを現在のマウスのx座標で初期化
objY = mouseY; //objY, disYを現在のマウスのy座標で初期化
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
//マウス座標とオブジェクトの距離をdisX, disYに入れる
disX = mouseX - objX;
disY = mouseY - objY;
//距離（disX, disY）をdelayで割った値を足す（オブジェクトが移動する）
objX = objX + disX/delay;
objY = objY + disY/delay;
ellipse(objX, objY, 20, 20);
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}これをまた少し変えてみましょう。今度はマウスをクリックしたらオブジェクトが後からついてくるサンプルです。
リスト4.7-d
float objX, objY; //オブジェクトのx, y座標
float disX, disY; //mouse座標とオブジェクトの距離
//mouseが押されたときに、一時的にx, y座標を保存しておくための変数
float targetX, targetY;
float delay = 20.0; //マウスに遅れる度合い
void setup() {
size(400, 400);
background(255);
noStroke();
fill(0);
objX = mouseX; //初期化
objY = mouseY;
targetX = targetY = 0.0;
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
//マウス座標とオブジェクトの距離をdisX, disYに入れる
disX = targetX - objX;
disY = targetY - objY;
//距離（disX, disY）をdelayで割った値を足す（オブジェクトが移動する）
objX = objX + disX/delay;
objY = objY + disY/delay;
ellipse(objX, objY, 20, 20);
}
void mousePressed() {
targetX = mouseX;
targetY = mouseY;
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}4.7.2 掴んで投げる
次のサンプルは、オブジェクトを掴んで離す際にマウスを移動したら、オブジェクトがその方向に飛んでいきます。また、オブジェクトが壁に当たって戻ってくるようにも書き換えることができます。
図4.7-d
リスト4.7-e
float objX, objY; //オブジェクトの座標
float velX, velY; //オブジェクトのスピード
void setup() {
size(400, 400);
background(255);
noStroke();
fill(0);
objX = objY = velX = velY = 0.0; //初期化
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
objX += velX; //x、y座標にvelX, velYの値を足す
objY += velY;
//このコードを実行すると、オブジェクトがバウンドする
if (objX > width || objX < 0) { //x方向に折り返す
velX = -velX;
}
if (objY > height || objY < 0) { //y方向に折り返す
velY = -velY;
}
///////////////////////////////////////
ellipse(objX, objY, 20, 20); //ellipseを描画
}
void mousePressed() { //オブジェクトの位置とスピードをリセット
velX = velY = 0.0;
objX = mouseX;
objY = mouseY;
}
void mouseDragged() {
objX = mouseX; //オブジェクトがマウスに追従する
objY = mouseY;
}
void mouseReleased() {
//pmouseXは前のフレームのマウスのx座標。
//この計算でマウスを動かしたスピードがわかる
velX = mouseX - pmouseX;
velY = mouseY - pmouseY;
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}4.7.3 マウス座標の方向に向く
結構需要があるのが、「オブジェクトがマウスの方向を向く」というアルゴリズムです。
ここでは、atan2()という関数がポイントになります。
atan2(y座標, x座標);この座標には、基準点を(0, 0)とした時のy座標、x座標を入れます。通常の関数の座標指定と違い、xとyの順序が逆であることに気をつけましょう。
図4.7-e
リスト4.7-f
float centerX; //基準点のx座標
float centerY; //基準点のy座標
void setup() {
size(400, 400);
stroke(0);
strokeWeight(5);
centerX = width/2; //基準点を画面中央に設定
centerY = height/2;
}
void draw() {
background(255);
//マウスから基準点の角度を計算
float angle = atan2(mouseY - centerY, mouseX - centerX);
//座標変換
translate(centerX, centerY); //画面中央に座標変換
pushMatrix();
rotate(angle); //angleの角度に座標変換
line(-100, 0, 100, 0);
popMatrix();
}4.7.4 マウスから逃げる
前述のイージングと基本的なアルゴリズムは同じですが、マウスが円に近づくと、近づいてきた方向と反対側に円が動きます。
ちょっと複雑ですが、atan2()という関数でマウスから円への角度を計算し、dist()という関数でマウスから円までの距離を計算しています。
図4.7-f
リスト4.7-g
float objX, objY; //オブジェクトのx, y座標
float disX, disY; //mouse座標とオブジェクトの距離
//マウスに遅れる度合い（2.0だと速すぎて見えないので20.0にしておく）
float delay = 20.0;
float targetX, targetY; //円の到達点
float rad; //円とマウス座標までの角度
float distance; //円とマウス座標の距離
float range = 100.0; //円が反応するマウス座標までの距離
void setup() {
size(400, 400);
background(255);
//現在のマウス座標で初期化
targetX = objX = width / 2;
targetY = objY = height / 2;
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
//可動範囲の枠
noFill();
stroke(0);
rect(20, 20, width - 40, height - 40);
//円からマウス座標までの角度
rad = atan2(objY - pmouseY, objX - pmouseX);
//円からマウス座標までの距離
distance = dist(mouseX, mouseY, objX, objY);
//距離がrange以内だったら新しい到達点を設定
if (distance < range) {
//objX, Yの値に新しく距離を加算
targetX = objX + distance*cos(rad);
targetY = objY + distance*sin(rad);
}
//マウス座標とオブジェクトの距離をdisX, disYに入れる
disX = targetX - objX;
disY = targetY - objY;
//距離をdelayで割った値を足す（オブジェクトが移動する）
objX += disX/delay;
objY += disY/delay;
//円は、画面の上下左右20pxで止まる
objX = min(max(objX, 20), width - 20);
objY = min(max(objY, 20), height - 20);
fill(0);
ellipse(objX, objY, 20, 20);
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}4.7.5 クリックで円のサイズがバウンドする
円をクリックすると拡大縮小を繰り返しながら、元のサイズに戻るサンプルです。R1は基準になる円の半径、R2は拡大縮小する範囲です。
図4.7-g
リスト4.7-h
float rad = 0.0; //角度を時間として扱う変数
float velocity = 0.1; //アニメーションのスピード
float damp = 0.98; //拡大縮小の減衰率
float maxSize = 100.0; //円の最大サイズ
float R1 = 100.0; //基準円のサイズ
float R2 = 0.0; //拡大縮小する範囲
void setup() {
size(400, 400);
noStroke();
fill(0);
}
void draw() {
background(255);
float r = R1 + R2*sin(rad); //円のサイズを計算
ellipse(width/2, height/2, r, r); //円を描画
rad += velocity; //時間を進める
if(rad > TWO_PI) rad = 0.0; //360度でリセット
R2 *= damp; //徐々に0に近づける
}
void mousePressed() {
rad = 0; //マウスを押すと時間をリセット
R2 = maxSize; //円のサイズを最大値にする
}