ゲームなどのプログラムでは、自然界の物理現象を数学的アルゴリズムによって再現したものがよく使われます。数式自体は比較的シンプルなものも多いので、ここでは、基礎的な物体の落下や放物線などのアルゴリズムを体験してみましょう。
4.6.1 重力
ボールが落下する運動です。重力(gravity)と反発力(reaction)を設定します。
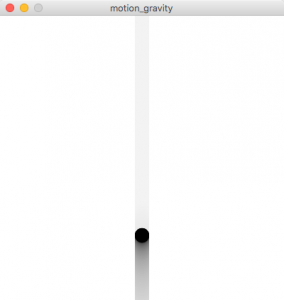
図4.6-a
リスト4.6-a
float y = 0.0; //ボールのy座標
float velocity = 0.0; //ボールの初速
float gravity = 0.1; //ボールにかかる重力
float reaction = 0.7; //ボールの反発力
void setup() {
size(400, 400);
background(255);
noStroke();
fill(0);
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
velocity += gravity; //スピードに重力が加算される
y += velocity; //ボールにスピードが設定される
if (y > height) { //もしボールが画面の下まで落ちたら、
velocity *= -reaction; //反発力によって上に上がる
y = height; //ボールは画面の外に外れない
}
ellipse(width/2, y, 20, 20); //ボールを描く
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}どうでしょうか。比較的シンプルなコードで、あたかも重力があるところに弾性のあるボールが落ちたかのような運動になっています。
4.6.2 放物線
次はもう少し複雑な運動になります。基本的には【リスト4.6-a】のサンプルにx軸方向の動きと摩擦を加えた形になります。

図4.6-b
リスト4.6-b
float x, y; //ボールのy座標
float velX = 5.0; //ボールのx軸の初速
float velY = 0.0; //ボールのy軸の初速
float gravity = 0.6; //ボールにかかる重力
float reaction = 0.7; //ボールの反発力
float damp = 0.9; //摩擦による減衰
void setup() {
size(300, 300);
background(255);
noStroke();
fill(0);
x = y = 0.0; //x, yを0.0で初期化
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
ellipse(x, y, 20, 20); //ボールを描く
velY += gravity; //スピードに重力が加算される
x += velX;//ボールにスピードを加算
y += velY;
//ボールが画面の横幅を超えたら反対の向きになる
if (x > width || x < 0) velX = -velX;
if (y > height) { //もしボールが画面の下まで落ちたら、
velY *= -reaction; //反発力によって上に上がる
velX *= damp; //velXを減衰
y = height; //ボールは画面の外に外れない
}
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}4.6.3 ばね
ばねの動きはシンプルな式によって求めることができます。フックの法則では
F = kx
・F = ばねの反発力
・k = ばねの強さ。ばね定数とも呼ばれる
・x = ばねが自然に停止する位置からの伸縮
で表されます。次のサンプルがその動きをコードにしたものです。マウスクリックで、円の位置がマウスのy座標まで移動します。
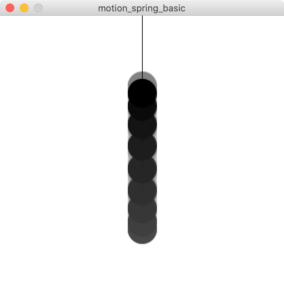
図4.6-c
リスト4.6-c
float y; //オブジェクトのy座標
float k = 0.1; //ばねの強さ
float velY = 0.0; //y方向のスピード
float force = 0; //ばねの反発力
float originY; //基準点
void setup() {
size(400, 400);
background(255);
y = 0; //開始時のオブジェクトのy座標は0
originY = 200; //ばねの長さは200
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
stroke(0);
line(width/2, 0, width/2, y);
float distY = originY - y; //基準点からの距離
force = k * distY; //ばねの力を計算(F = kx)
velY += force; //ばねの力をスピードに足す
y += velY; //オブジェクトを移動
fill(0);
ellipse(width/2, y, 40, 40); //円を描画
}
//クリックで円の位置をマウスのy座標にする
void mousePressed() {
y = mouseY;
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
stroke(255, 10);
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}このコードだと永遠に動き続けるので「摩擦による減衰」と、「ばねの先のオブジェクトの重さ」による加速を追加します。
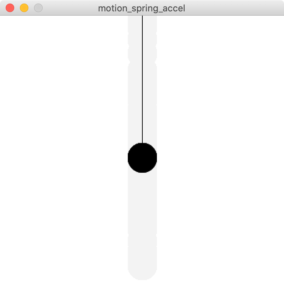
図4.6-d
リスト4.6-d
float y; //オブジェクトのy座標
float mass = 10.1; //オブジェクトの質量
float k = 0.3; //ばねの強さ(ばね定数)
float damp = 0.97; //摩擦による減衰率
float velY = 0.0; //y方向のスピード
float accel = 0; //加速度
float force = 0; //ばねの反発力
float originY; //基準点
void setup() {
size(400, 400);
background(255);
y = 0; //開始時のオブジェクトのy座標は0
originY = 200; //ばねの長さは200
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
stroke(0);
line(width/2, 0, width/2, y);
float distY = originY - y; //基準点からの距離
force = k * distY; //ばねの力を計算(F = kx)
accel = force / mass; //重さによる加速度を計算
velY = damp * (velY + accel); //摩擦による減衰を計算
y += velY; //オブジェクトを移動
fill(0);
ellipse(width/2, y, 40, 40); //円を描画
}
//クリックで円の位置をマウスのy座標にする
void mousePressed() {
y = mouseY;
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
stroke(255, 10);
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}最後にx方向にも動気をつけて、さらにマウスに追従するようにしてみます。
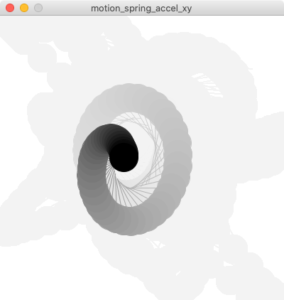
図4.6-e
リスト4.6-e
float x, y; //オブジェクトのy座標
float mass = 2.5; //オブジェクトの質量
float k = 0.1; //ばねの強さ(ばね定数)
float damp = 0.9; //摩擦による減衰率
float velX, velY; //y方向のスピード
float accelX, accelY; //加速度
float forceX, forceY; //ばねの反発力
float originX, originY; //基準点
void setup() {
size(400, 400);
background(255);
x = originX = width / 2; //開始時の円の位置を画面中央で初期化
y = originY = height / 2;
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
stroke(0);
line(x, y, mouseX, mouseY);
originX = mouseX; //ばねの基準点をマウス座標にする
originY = mouseY;
float distX = originX - x; //基準点からの距離
forceX = k * distX; //ばねの力を計算(F = kx)
accelX = forceX / mass; //重さによる加速度を計算
velX = damp * (velX + accelX); //摩擦による減衰を計算
x += velX; //オブジェクトを移動
float distY = originY - y; //基準点からの距離
forceY = k * distY; //ばねの力を計算(F = kx)
accelY = forceY / mass; //重さによる加速度を計算
velY = damp * (velY + accelY); //摩擦による減衰を計算
y += velY; //オブジェクトを移動
fill(0);
ellipse(x, y, 40, 40); //円を描画
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
stroke(255, 10);
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}4.6.4 振り子
振り子の場合は、もう少し複雑なアルゴリズムになります。
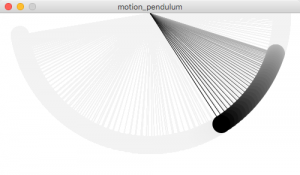
図4.6-f
リスト4.6-f
float x, y; //円の座標
float R = 220; //回転半径
float rad = -0.5*PI; //スタート時の回転角
float angle_vel = 0.0; //角速度
float gravity = 0.3; //重力
float angle_accel; //角加速度
float damp = 0.998; //減衰率
void setup() {
size(500, 270);
background(255);
noStroke();
fill(0);
}
void draw() {
//フェードする時はtrue、しない場合はfalse
fade(false);
//角加速度は、(-1*重力/回転半径)*sin(角度)
angle_accel = (-1*gravity/R)*sin(rad); //角加速度を計算
angle_vel += angle_accel; //角速度を計算
//angle_vel *= damp; //減衰率を計算
rad += angle_vel; //角度に角速度を計算
//一番下は円の角度だと90度(-90度ではない。プログラムの場合はy方向が反対)。
//ラジアンにすると0.5PIなので、計算結果に90度足している。
x = R*cos(rad + 0.5*PI);
y = R*sin(rad + 0.5*PI);
stroke(0);
line(width/2, 0, x + width/2, y); //線
noStroke();
ellipse(x + width/2, y, 30, 30); //円
}
//フェード用関数
void fade(boolean _fadeFlag) {
if (_fadeFlag) {
fill(255, 10); //透明度のあるrectを描画
rect(0, 0, width, height);
fill(0); //オブジェクトは黒
} else {
background(255);
}
}このコードをそのまま再生すると、摩擦による減衰が考慮されていないためずっと動き続けます。そこで、24行目(//angle_vel *= damp;)のコメントアウトを外して角速度を減衰してください。かなりリアルな振り子の動きになります。
angle_vel *= damp; //減衰率を計算1 | angle_vel *= damp; //減衰率を計算 |
